Class 9 Maths
Number Systems

Introduction
Number system is system of Numeration. It is a writing system for expressing number. Typically used to count numbers, measure temperature, find area of an object, and numerically represent any data.
The classification is based on History of numbers.
Natural Numbers: Natural numbers were the first to come. They are denoted by N. These numbers can be counted on fingers. E.g.: 1, 2, 3, 4, 5, 6, 10, 15, 20, 21 etc
Whole Number: Aryabahatta, famous Mathematician gave ‘0’ to the number system. It is very powerful number. Anything multiplied by 0 becomes 0. This new number 0, when added to the Natural numbers gave a new set of numbers called Whole number. E.g.: 0, 2, 3 5 etc. It is denoted by W. It has all natural numbers plus 0. Note that Whole number has only positive numbers. All Natural numbers are whole number but the reverse is not true.
Integers: Field of Mathematics advanced & there was a need for Negative numbers as well. If we add negative numbers to the whole number, we get Integers. It is denoted by “Z”. Z came from word Zahlen that means “to count”. It is used to express temperature, latitude, longitude etc which can have negative values. E.g.: -20oC. All Whole numbers are Integers, but the reverse is not true. Refer the image below for clarity.
Rational Numbers: Field of Mathematics advance further & concept of division came into picture. Numbers that can be represented in the form of p/q where P& Q are Integers & q≠ 0 were called Rational Number. Word Rational number came from Ratio. It is demoted by Q. Q letter is taken from word Quotient. E.g.: ½, 9/5 etc. There is Infinite Rational Numbers between any 2 Rational Numbers. All Integers are Rational Number , but the reverse is not true.
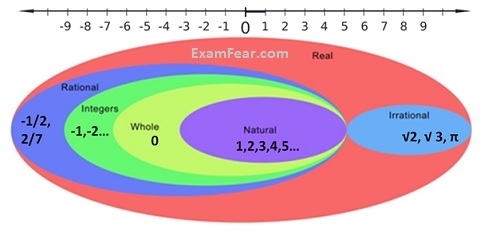
Irrational Numbers: Field of Mathematics advance further & mathematicians found that there are some numbers that can’t be written in the form of p/q where p& q are integers & q≠0. They call it irrational Numbers. Eg √2, √3
Real number: Both Rational & Irrational Numbers together forms Ream number. It is denoted by R. Evert point on the number line is a Real number. E.g.: √2, -7, 4/9 , 0, 5 etc. All rational numbers are real number. All irrational numbers are real number, but the reverse is not true.
Class 9 Maths Number Systems NCERT Chapter 1 Free Notes for Best Revision
Revision of Class 9 Maths Number Systems is a crucial aspect of effective learning. Revision plays a vital role in the learning process and is especially important before exams. Here are some key points you can consider emphasizing in your content:
- Retention and Memory: Regularly reviewing and revisiting the material of Class 9 Maths Number Systems helps reinforce the concepts in students' minds. It strengthens memory pathways, making it easier to recall information during exams and beyond.
- Consolidation of Knowledge: When you revise notes, you are essentially consolidating your knowledge. This means connecting new information with what you already know, making the overall understanding more robust.
- Identifying Knowledge Gaps: Revision allows students to identify any gaps in their understanding or areas where they need further clarification. This gives you a chance to seek help or delve deeper into those topics. For detailed understanding, you can always refer to the videos of Number Systems Class 9 Maths NCERT Chapter 1 on LearnoHub.com
- Building Confidence: As you revise Number Systems Class 9 Maths and become more familiar with the content, your confidence in your abilities grows. Confidence is a crucial factor in exam performance as it reduces anxiety and allows you to approach exams with a positive mindset.
- Different Revision Techniques: Use a variety of revision techniques such as summarizing notes, creating flashcards, practicing past papers, discussing concepts with peers, and teaching others. Different techniques work for different students, and it's essential to find what suits you the best. You can also attend the LIVE Revision classes on LearnoHub.com or watch the LIVE Revision Race videos of LearnoHub on Number Systems Class 9 Maths NCERT Chapter 1.
- Spacing Effect: Spacing out revision sessions over time, rather than cramming all at once, has been shown to improve long-term retention. Create a revision schedule leading up to the exams to allow for spaced practice.
- Regular Revision over Cramming: Regular and consistent revision throughout the academic year is very important. Waiting until the last moment to cram everything can be overwhelming and less effective than spaced-out revision.
- Self-Assessment: Assess your understanding periodically through quizzes or self-tests. This helps you to gauge your progress and identify areas that need further attention. Refer Class 9 Number Systems Online Tests.
- Balanced Approach: Remind students to strike a balance between revision and other activities. Adequate rest, exercise, and relaxation are essential for optimal learning and performance.
- Seeking Help: If you face difficulties during the revision process, Refer the videos of Class 9 Maths Number Systems. Clearing doubts promptly is crucial for a better grasp of the subject matter. You can always ask your doubts on Number Systems Class 9 Maths NCERT Chapter 1. “Ask a Question” section of LearnoHub.com
By highlighting the benefits and strategies of effective revision, you can approach your studies more mindfully and achieve better results in your exams. Best of luck bachhon!
Class 9 Maths seems to be a quite difficult subject for a lot of students. But, if you get a very good conceptual understanding of the subject, it can be very interesting for you.
We, at LearnoHub, will give our best to make Class 9 Maths Number Systems NCERT Chapter 1 super-duper easy for you.
We aim at making learning fun as well as engaging for you with our complete end-end learning content with Number Systems Class 9 Maths Best videos, Notes, NCERT pdf, NCERT complete syllabus, tests and Practice Questions.
Always remember, it is very important to study with full concentration during Revision. Here are a few tips for you on how to revise with full focus:
- Create a Distraction-Free Environment: Find a quiet and comfortable place to study where you can minimize distractions. Turn off or silence your phone, log out of social media accounts, and inform others around you that you need uninterrupted study time. A dedicated study environment will help you focus better.
- Set Specific Goals: Before starting your study session, set clear and achievable goals. Break down your study material into smaller tasks, and plan what you want to accomplish during each session. Having specific goals will give you a sense of direction and purpose, making it easier to concentrate.
- Use the Pomodoro Technique: The Pomodoro Technique is a time management method that involves studying in short, focused intervals, typically 25 minutes, followed by a short break of 5 minutes. After completing four sessions, take a longer break of around 15-30 minutes. This technique can improve focus and productivity by providing regular breaks to recharge.
- Stay Organized: Keep your study materials, notes, and resources well-organized. Having everything you need at hand will save time and reduce distractions caused by searching for materials. Use color-coded folders or digital tools to maintain a structured study system.
- Practice Mindfulness and Meditation: Before you begin studying, take a few minutes to practice mindfulness or meditation. Deep breathing exercises and clearing your mind of distractions can help you approach your study session with a calm and focused mindset.
Remember, studying with full concentration is a skill that takes time and practice to develop. If you find your mind wandering during study sessions, gently bring your focus back to the task at hand and be patient with yourself. With consistent effort, you can improve your ability to concentrate and make the most of your study time.
Last but not the least, To get the best hold on Class 9 Maths Number Systems Book Chapter 1. Do not forget to check out:
- Number Systems Class 9 Maths Best videos
- Number Systems Class 9 Maths NCERT Solutions
- Class 9 Maths Number Systems Revision notes
- Number Systems Class 9 Maths DPPS, Download PDF of solutions
- Class 9 Maths Number Systems Online Tests
- Class 9 Maths Sample papers