Revise notes Class 12 continuity and differentiability

Revise notes
Class 12 Maths
Continuity and Differentiability

Topics

1. Introduction to Continuity
2. Differentiability
3. Exponential and Logarithmic Functions
4. Logarithmic Differentiation
5. Derivatives of Functions in Parametric Forms
6. Second Order Derivative
7. Mean Value Theorem

Mean Value Theorem

There are two fundamental results in Calculus. We will discuss both of them and also learn the geometric interpretation of these theorems.

Rolle’s Theorem:

Let f be a real valued function defined on the closed interval [a, b] such that

(i) It is continuous on the closed interval [a, b].

(ii) It is differentiable on the open interval (a, b)

(iii) f(a) = f(b)

Then there exists a real number c є (a, b) such that f′(c) = 0.

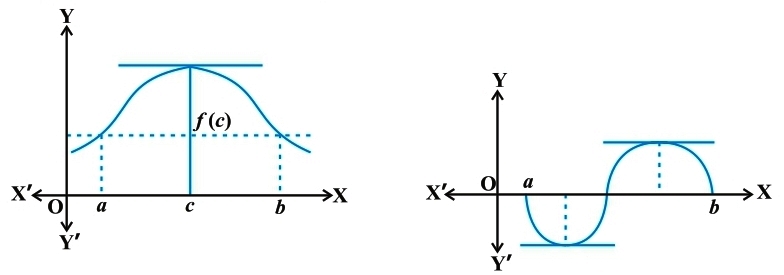
Class_12_Maths_Continuity_&_Differentiability

In each of the above graph, the slope becomes zero at least at one point. That is precisely the claim of the Rolle’s theorem as the slope of the tangent at any point on the graph of y = f (x) is nothing but the derivative of f(x) at that point.

Problem: Verify Rolle’s Theorem for the function f(x) = x² + 2x – 8, x ∈ [-4, 2]

Solution:

The given function f(x) = x² + 2x – 8 being a polynomial function, is continuous in [−4, 2] and is differentiable in (−4, 2).

f(-4) = (-4)² + 2 * (-4) – 8 = 16 – 8 – 8 = 0

f(2) = 2² + 2 * 2 – 8 = 4 + 4 – 8 = 0

So, f (−4) = f (2) = 0

=> The value of f (x) at −4 and 2 coincides.

Rolle’s Theorem states that there is a point c ∈ (−4, 2) such that f’(c) = 0

Now, f(x) = x² + 2x – 8

f’(x) = 2x + 2

Now, f’(c) = 0

=> 2c + 2 = 0

=> c = -1, where c ∈ (−4, 2)

Hence, Rolle’s Theorem is verified for the given function.

Mean Value Theorem:

Let f be a real valued function defined on the closed interval [a, b] such that

(i) It is continuous on the closed interval [a, b].

(ii) It is differentiable on the open interval (a, b)

(iii) f(a) = f(b)

Then there exists a real number c є (a, b) such that f′(c) = {f(b) – f(a)}/(b - a)

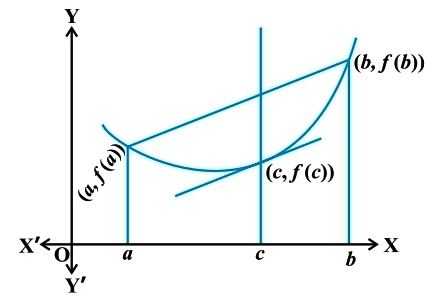
Class_12_Maths_Continuity_&_Differentiability_Mean_Value_Therorem

This theorem is an extension of Rolle’s theorem. From the graph, it is clear that {f(b) – f(a)}/(b - a) is the slope of the secant drawn between (a, f(a)) and (b, f(b)). The theorem stats that there is a point c in (a, b) such that the tangent at (c, f(c)) is parallel to the secant between (a, f(a)) and (b, f(b)).

Problem: Verify Mean Value Theorem, if f(x) = x² – 4x – 3 in the interval [a, b], where a = 1 and b = 4.

Solution: The given function is f(x) = x² – 4x – 3

The polynomial function f is continuous in [1, 4] and is differentiable in (1, 4) whose derivative is 2x − 4.

f(1) = 1² – 4 * 1 – 3 = 1 – 4 – 3 = -6

f(4) = 4² – 4 * 4 – 3 = 16 – 16 – 3 = -3

So, {f(b) –f(a)}/(b - a) = {f(4) –f(1)}/(4 - 1) = {-3 – (-6)}/3 = (-3 + 6)/3 = 3/3 = 1

Mean Value Theorem states that there is a point c ∈ (1, 4) such that f’(c) = 1

=> 2c – 4 = 1

=> 2c = 5

=> c = 5/2, where c = 5/2 ∈ (1, 4)

Hence, Mean Value Theorem is verified for the given function.

← Prev

Class 12 Maths Continuity and Differentiability NCERT Chapter 5 Free Notes for Best Revision

Revision of Class 12 Maths Continuity and Differentiability is a crucial aspect of effective learning. Revision plays a vital role in the learning process and is especially important before exams. Here are some key points you can consider emphasizing in your content:

Retention and Memory: Regularly reviewing and revisiting the material of Class 12 Maths Continuity and Differentiability helps reinforce the concepts in students' minds. It strengthens memory pathways, making it easier to recall information during exams and beyond.
Consolidation of Knowledge: When you revise notes, you are essentially consolidating your knowledge. This means connecting new information with what you already know, making the overall understanding more robust.
Identifying Knowledge Gaps: Revision allows students to identify any gaps in their understanding or areas where they need further clarification. This gives you a chance to seek help or delve deeper into those topics. For detailed understanding, you can always refer to the videos of Continuity and Differentiability Class 12 Maths NCERT Chapter 5 on LearnoHub.com
Building Confidence: As you revise Continuity and Differentiability Class 12 Maths and become more familiar with the content, your confidence in your abilities grows. Confidence is a crucial factor in exam performance as it reduces anxiety and allows you to approach exams with a positive mindset.
Different Revision Techniques: Use a variety of revision techniques such as summarizing notes, creating flashcards, practicing past papers, discussing concepts with peers, and teaching others. Different techniques work for different students, and it's essential to find what suits you the best. You can also attend the LIVE Revision classes on LearnoHub.com or watch the LIVE Revision Race videos of LearnoHub on Continuity and Differentiability Class 12 Maths NCERT Chapter 5.
Spacing Effect: Spacing out revision sessions over time, rather than cramming all at once, has been shown to improve long-term retention. Create a revision schedule leading up to the exams to allow for spaced practice.
Regular Revision over Cramming: Regular and consistent revision throughout the academic year is very important. Waiting until the last moment to cram everything can be overwhelming and less effective than spaced-out revision.
Self-Assessment: Assess your understanding periodically through quizzes or self-tests. This helps you to gauge your progress and identify areas that need further attention. Refer Class 12 Continuity and Differentiability Online Tests.
Balanced Approach: Remind students to strike a balance between revision and other activities. Adequate rest, exercise, and relaxation are essential for optimal learning and performance.
Seeking Help: If you face difficulties during the revision process, Refer the videos of Class 12 Maths Continuity and Differentiability. Clearing doubts promptly is crucial for a better grasp of the subject matter. You can always ask your doubts on Continuity and Differentiability Class 12 Maths NCERT Chapter 5. “Ask a Question” section of LearnoHub.com

By highlighting the benefits and strategies of effective revision, you can approach your studies more mindfully and achieve better results in your exams. Best of luck bachhon!

Class 12 Maths seems to be a quite difficult subject for a lot of students. But, if you get a very good conceptual understanding of the subject, it can be very interesting for you.

We, at LearnoHub, will give our best to make Class 12 Maths Continuity and Differentiability NCERT Chapter 5 super-duper easy for you.

We aim at making learning fun as well as engaging for you with our complete end-end learning content with Continuity and Differentiability Class 12 Maths Best videos, Notes, NCERT pdf, NCERT complete syllabus, tests and Practice Questions.

Always remember, it is very important to study with full concentration during Revision. Here are a few tips for you on how to revise with full focus:

Create a Distraction-Free Environment: Find a quiet and comfortable place to study where you can minimize distractions. Turn off or silence your phone, log out of social media accounts, and inform others around you that you need uninterrupted study time. A dedicated study environment will help you focus better.
Set Specific Goals: Before starting your study session, set clear and achievable goals. Break down your study material into smaller tasks, and plan what you want to accomplish during each session. Having specific goals will give you a sense of direction and purpose, making it easier to concentrate.
Use the Pomodoro Technique: The Pomodoro Technique is a time management method that involves studying in short, focused intervals, typically 25 minutes, followed by a short break of 5 minutes. After completing four sessions, take a longer break of around 15-30 minutes. This technique can improve focus and productivity by providing regular breaks to recharge.
Stay Organized: Keep your study materials, notes, and resources well-organized. Having everything you need at hand will save time and reduce distractions caused by searching for materials. Use color-coded folders or digital tools to maintain a structured study system.
Practice Mindfulness and Meditation: Before you begin studying, take a few minutes to practice mindfulness or meditation. Deep breathing exercises and clearing your mind of distractions can help you approach your study session with a calm and focused mindset.

Remember, studying with full concentration is a skill that takes time and practice to develop. If you find your mind wandering during study sessions, gently bring your focus back to the task at hand and be patient with yourself. With consistent effort, you can improve your ability to concentrate and make the most of your study time.

Last but not the least, To get the best hold on Class 12 Maths Continuity and Differentiability Book Chapter 5. Do not forget to check out:

Continuity and Differentiability Class 12 Maths Best videos
Continuity and Differentiability Class 12 Maths NCERT Solutions
Class 12 Maths Continuity and Differentiability Revision notes
Continuity and Differentiability Class 12 Maths DPPS, Download PDF of solutions
Class 12 Maths Continuity and Differentiability Online Tests
Class 12 Maths Sample papers