Class 8 Maths
Understanding Quadrilaterals

Ex. 3.1 Q1.
Given here are some figures:
Classify each of them on the basis of the following:
(a) Simple curve
(b) Simple closed curve
(c) Polygon
(d) Convex polygon
(e) Concave polygon
View Answer
Ex. 3.1 Q2.
How many diagonals does each of the following have?
(a) A convex quadrilateral
(b) A regular hexagon
(c) A triangle
View Answer
Ex. 3.1 Q3.
What is the sum of the measures of the angles of a convex quadrilateral? Will this property hold if the quadrilateral is not convex? (Make a non-convex quadrilateral and try)
View Answer
Ex. 3.1 Q4.
Examine the table. (Each figure is divided into triangles and the sum of the angles deduced from that.)
What can you say about the angle sum of a convex polygon with number of sides?
View Answer
Ex. 3.1 Q5.
What is a regular polygon? State the name of a regular polygon of:
(a) 3 sides
(b) 4 sides
(c) 6 sides
View Answer
Ex. 3.1 Q6.
Find the angle measures x in the following figures:
View Answer
Ex. 3.1 Q7.
(a) Find x + y + z
(b) Find x + y + z + w
View Answer
Ex. 3.2 Q1.
Find x in the following figures:
View Answer
Ex. 3.2 Q2.
Find the measure of each exterior angle of a regular polygon of:
(a) 9 sides
(b) 15 sides
View Answer
Ex. 3.2 Q3.
How many sides does a regular polygon have, if the measure of an exterior angle is 240?
View Answer
Ex. 3.2 Q4.
How many sides does a regular polygon have if each of its interior angles is 1650?
View Answer
Ex. 3.2 Q5.
(a) Is it possible to have a regular polygon with of each exterior angle as 220?
(b) Can it be an interior angle of a regular polygon? Why?
View Answer
Ex. 3.2 Q6.
(a) What is the minimum interior angle possible for a regular polygon? Why?
(b) What is the maximum exterior angle possible for a regular polygon?
View Answer
Ex. 3.3 Q1.
Given a parallelogram ABCD. Complete each statement along with the definition or property used.
(i) AD = ____________________
(ii) Ð DCB = ____________________
(iii) OC = ____________________
(iv) mÐ DAB + mÐ CDA = ____________________
View Answer
Ex. 3.3 Q2.
Consider the following parallelograms. Find the values of the unknowns x, y, z.
Note: For getting correct answer, read 30 = 300 in figure (iii)
View Answer
Ex. 3.3 Q3.
Can a quadrilateral ABCD be a parallelogram, if:
(i) ÐD + ÐB = 1800?
(ii) AB = DC = 8 cm, AD = 4 cm and BC = 4.4 cm?
(iii) Ð A = 70 and Ð C = 650?
View Answer
Ex. 3.3 Q4.
Draw a rough figure of a quadrilateral that is not a parallelogram but has exactly two opposite angles of equal measures.
View Answer
Ex. 3.3 Q5.
The measure of two adjacent angles of a parallelogram are in the ratio 3 : 2. Find the measure of each of the angles of the parallelogram.
View Answer
Ex. 3.3 Q6.
Two adjacent angles of a parallelogram have equal measure. Find the measure of the angles of the parallelogram.
View Answer
Ex. 3.3 Q7.
The adjacent figure HOPW is a parallelogram. Find the angle measures x, y and z. State the properties you use to find them.
View Answer
Ex. 3.3 Q8.
The following figures GUNS and RUNS are parallelograms. Find x and y. (Lengths are in cm)
View Answer
Ex. 3.3 Q9.
In the figure, both RISK and CLUE are parallelograms. Find the value of x.
View Answer
Ex. 3.3 Q10.
Explain how this figure is a trapezium. Which is its two sides are parallel?
View Answer
Ex. 3.3 Q11.
Find mÐ C in figure , if 𝐴𝐵 || 𝐷𝐶.
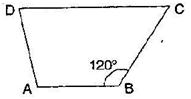
View Answer
Ex. 3.3 Q12.
Find the measure of Ð P and Ð S if 𝑆𝑃 || 𝑅𝑄 in given figure.
(If you find mÐ R is there more than one method to find mÐ P)
View Answer
Ex. 3.4 Q1.
State whether true or false:
(a) All rectangles are squares.
(b) All rhombuses are parallelograms.
(c) All squares are rhombuses and also rectangles.
(d) All squares are not parallelograms.
(e) All kites are rhombuses.
(f) All rhombuses are kites.
(g) All parallelograms are trapeziums.
(h) All squares are trapeziums.
View Answer
Ex. 3.4 Q2.
Identify all the quadrilaterals that have:
(a) four sides of equal lengths.
(b) four right angles.
View Answer
Ex. 3.4 Q3.
Explain how a square is:
(i) a quadrilateral
(ii) a parallelogram
(iii) a rhombus
(iv) a rectangle
View Answer
Ex. 3.3 Q4.
Name the quadrilateral whose diagonals:
(i) bisect each other.
(ii) are perpendicular bisectors of each other.
(iii) are equal.
View Answer
Ex. 3.4 Q5.
Explain why a rectangle is a convex quadrilateral.
View Answer
Ex. 3.4 Q6.
ABC is a right-angled triangle and O is the mid-point of the side opposite to the right angle. Explain why O is equidistant from A, B and C. (The dotted lines are drawn additionally to help you.)
View Answer