NCERT solution Class 10 areas related to circles

NCERT Solutions

Class 10 Maths

Areas Related to Circles

NCERT Questions

Ex.11.1 Q.1
Ex.11.1 Q.2
Ex.11.1 Q.3
Ex.11.1 Q.4
Ex.11.1 Q.5
Ex.11.1 Q.6
Ex.11.1 Q.7
Ex.11.1 Q.8
Ex.11.1 Q.9
Ex.11.1 Q.10
Ex.11.1 Q.11
Ex.11.1 Q.12
Ex.11.1 Q.13
Ex.11.1 Q.14

Ex.11.1 Q.13

A round table cover has six equal designs as shown in Fig. 12.14. If the radius of the cover is 28 cm, find the cost of making the designs at the rate of Rs 0.35 per cm2. (Use √3 = 1.7)

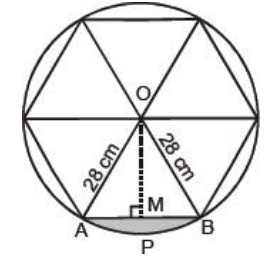
Here, r = 28 cm

Since, the circle is divided into six equal sectors.

So, sector angle θ = 360° ÷ 6 = 60°

Area of the sector with angle 60° and radius 28 cm = (θ ÷ 360°) × πr2

= (60° ÷ 360°) × ( ) × 28 × 28

= ( ) x × 28 × 4

= (44 × 28) ÷ 3

= 410.67 cm2 …………… (1)

Now, area of 1 design = Area of segment APB

= Area of sector – Area of ΔAOB …………... (2)

In ΔAOB, ∠AOB = 60°, OA = PN = 28 cm

So, ∠OAB = 60° and ∠OBA = 60°

=> ΔAOB is an equilateral triangle.

=> AB = AO = BO

=> AB = 28 cm

=> Draw OM ⊥AB

Now, in right ΔAOM, we have

= sin 60° =

=> OM = OA ×

=> OM = 28 ×

=> OM = 14√3 cm

Area of ΔAOB = × AB × OM

= × 28 × 14√3

= 14 × 14 × 1.7

= 333.3 cm2 ………... (3)

Now, from (1), (2) and (3), we have:

Area of segment APQ = 410.67 – 333.2

= 77.47 cm2

=> Area of 1 design = 77.47 cm2

So, area of the 6 equal designs = 6 × 77.47

= 464.82 cm2

Cost of making the design at the rate of Rs. 0.35 per cm2 = Rs. 0.35 × 464.82

= Rs. 162.68

Video solution:

Areas Related to Circles Class 10 Maths NCERT Chapter 12 NCERT Solutions

Solving NCERT textbook questions of Areas Related to Circles Class 10 Maths NCERT Chapter 12 is a crucial step to gauge your understanding of the concepts. It provides you with an opportunity to assess your grasp of the material after learning each chapter. We have already provided solutions to all the exercises in the NCERT textbook of Class 10 Maths Areas Related to Circles, available in various formats such as video, text, and downloadable PDFs. If you need assistance with any of the NCERT questions or any other academic topics, feel free to ask in the “Ask Questions” section of LearnoHub.com.

Studying each and every line of the NCERT (National Council of Educational Research and Training) textbook of Areas Related to Circles Class 10 Maths and solving all the questions it contains can be highly beneficial for several reasons:

Comprehensive Understanding: Class 10 Maths NCERT textbooks are designed by experts to provide a comprehensive understanding of the subject matter. By studying each line of Areas Related to Circles Class 10 Maths, you ensure that you don't miss any essential information or concepts.
Strong Foundation: NCERT books form the foundation of many academic exams and competitive tests. Mastering these textbooks helps build a solid foundation of knowledge for higher-level studies.
Clarity of Concepts: Solving the questions provided in NCERT textbooks for Areas Related to Circles Class 10 Maths NCERT Chapter 12 reinforces the concepts learned in each chapter. It helps you apply theoretical knowledge to practical problem-solving scenarios.
Exam Preparation: Many standardized tests, including board exams and entrance exams, extensively rely on NCERT content. Familiarity with the textbook content and practice with its questions can enhance your exam performance.
Common Language: NCERT textbooks use simple and easily understandable language. Mastering the material ensures you are well-versed in the language commonly used in various academic and competitive settings.
Confidence Boost: Successfully solving all the NCERT questions of Areas Related to Circles Class 10 Maths gives you a sense of accomplishment and boosts your confidence in your knowledge and problem-solving skills.
In-Depth Learning: Delving into each line of the textbook for the chapter Areas Related to Circles Class 10 Maths helps you gain in-depth knowledge of the subject, making you better prepared to tackle complex problems and real-life situations.
Time Management: By thoroughly studying and solving all the NCERT questions, you develop efficient time management skills, which are crucial during exams when you need to answer questions within a limited time frame.
Holistic Approach: NCERT textbooks usually cover a wide range of topics, providing a holistic understanding of the subject. This approach is essential for a well-rounded education.
Application in Real Life: The concepts and knowledge gained from NCERT textbooks often have practical applications in everyday life, helping you make informed decisions and solve real-world challenges.

In conclusion, studying each line and solving all the questions of NCERT textbooks is an essential part of the learning process. It ensures a strong foundation, deep understanding, and overall academic growth.

How to make the most of NCERT Solutions module of Areas Related to Circles Class 10 Maths NCERT Chapter 12 on LearnoHub.com?

Using the NCERT solutions module effectively can significantly enhance your learning experience and understanding of the subject matter. Here's a step-by-step guide on how to make the most out of the NCERT solutions:

Attempt to Solve Yourself: Before looking at the solution, try to solve or answer the question independently. This practice will help you test your knowledge and problem-solving skills.
Match with Our Solution: After attempting the question, compare your result and approach with the provided NCERT solution. This step allows you to identify any mistakes or gaps in your understanding.
Refer to Solution Video (if needed): If you encounter difficulty or are unable to solve a question, you can refer to the NCERT solution video on Areas Related to Circles Class 10 Maths NCERT Chapter 12 to get a step-by-step explanation of the correct approach. Pay attention to the reasoning and methodology used in the video.
Solve Again Yourself: Once you've understood the solution, attempt to solve the question again by yourself. Repetition and practice solidify your understanding of the concepts and improve retention.
Avoid Memorization: Focus on understanding the underlying principles and concepts behind each solution. Avoid simply memorizing the solutions, as this may hinder your ability to apply the knowledge in different contexts.
Attempt All Questions: Make an effort to attempt all the questions provided in the NCERT textbook. This comprehensive practice will help you cover the entire syllabus and reinforce your understanding across various topics. You may refer Class 10 Maths Areas Related to Circles Online Test on LearnoHub.com.
Review and Revise: Regularly review the concepts and solutions you've learned. Revise your notes and practice regularly to retain the knowledge effectively. You may refer Areas Related to Circles Class 10 Maths Notes.
Ask for Clarification: If you encounter any doubts or have questions about the solutions, don't hesitate to seek clarification on the “Ask Questions” section of LearnoHub.com. Areas Related to Circles Class 10 Maths NCERT Chapter 12 Questions.

By following these steps and actively engaging with the NCERT solutions module of Class 10 Maths Areas Related to Circles NCERT Chapter 12, you can improve your learning outcomes, develop a better grasp of the subject, and perform well in exams and other academic assessments. Remember that consistent practice, understanding, and application of knowledge are key to academic success.

NCERT solutions of Areas Related to Circles Class 10 Maths - all questions of all exercises are solved. Q. No. 1, 2, 3, and so on. Complete explanation and detailed solution makes them the best videos for Class 10 Maths Areas Related to Circles NCERT solutions.