According to the kinetic theory of gas,

- Gases are composed of very small molecules and their number of molecules is very large.
- These molecules are elastic.
- They are negligible size compare to their container.
- Their thermal motions are random.

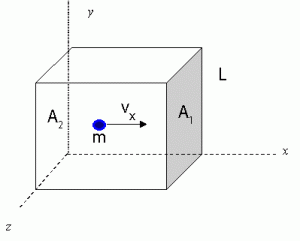
To begin, let us visualize a rectangular box with length L, areas of ends A₁ and A₂. There is a single molecule with speed v_x traveling left and right to the end of the box by colliding with the end walls.

n, let us visualize a rectangular box with length L, areas of ends A₁ and A₂. There is a single molecule with speed v_x traveling left and right to the end of the box by colliding with the end walls.

3D Demonstration of Ideal Gas

The time between collisions with the wall is the distance of travel between wall collisions divided by the speed.

1.

The frequency of collisions with the wall in collisions per second is

2.

According to Newton, force is the time rate of change of the momentum

3.

The momentum change is equal to the momentum after collision minus the momentum before collision. Since we consider the momentum after collision to be mv, the momentum before collision should be in opposite direction and therefore equal to -mv.

4.

According to equation 3, force is the change in momentum divided by change in time .  To get an equation of average force in term of particle velocity , we take change in momemtum multiply by the frequency from equation 2. 

5.

The pressure, P, exerted by a single molecule is the average force per unit area, A. Also V=AL which is the volume of the rectangular box.

6.

Let us say that we have N molecules of gas traveling on the x-axis. The pressure will be

7.

To simplify the situation we will take the mean square speed of N number of molecules instead of summing up individual molecules. Therefore, equation 7 will become

8. 

Earlier we are trying to simplify the situation by only considering that a molecule with mass m is traveling on the x axis.  However, the real world is much more complicated than that. To make a more accurate derivation we need to account all 3 possible components of the particles speed, v_x, v_y and v_z.

9.

Since there are a large number of molecules we can assume that there are equal numbers of molecules moving in each of co-ordinate directions.

10.

Because the molecules are free too move in three dimensions, they will hit the walls in one of the three dimensions one third as often. Our final pressure equation becomes 

11.

However to simplify the equation further, we define the temperature, T, as a measure of thermal motion of gas particles because temperature is much easier to measure than the speed of the particle. The only energy involve in this model is kinetic energy and this kinetic enery is proportional to the temperature T. 

12.

To combine the equation 11 and 12 we solve kinetic energy equation 12 for mv². 

13.

Since the temperature can be obtained easily with simple daily measurement like a thermometer, we will now replace the result of kinetic equation #13 with with a constant R times the temperature, T. Again, since T is proportional to the kinentic energy it is logical to say that T times k is equal to the kinetic energy E. k, however, will currently remains unknown.

14.

Combining equation 14 with 11, we get:

15.

Because a molecule is too small and therefore impractical we will take the number of molecules, N and divide it by the Avogadros number, N_A= 6.0221 x 10²³/mol to get n (the number of moles)

16.

Since N is divided by N_a, k must be multiply by N_a to preserve the original equation. Therefore, the constant R is created.

17.

Now we can achieve the final equation by replacing N (number of melecules) with n (number of moles) and k with R. 

17.

Calculation of R & k

According to numerous tests and observations, one mole of gas is a 22.4 liter vessel at 273K exerts a pressure of 1.00 atmosphere (atm). From the ideal gas equation above:

A.

B.

C.